Unfolding secrets of Matrix multiplication
- StatisticaHub
- Mar 30, 2023
- 4 min read
Updated: Jun 13, 2024
Linear algebra is one of the cornerstones of machine learning. It’s more intuitive than you might think.
“The goal here is not to try to teach everything, it’s that you come away with a strong intuition… and that those intuitions make any future learning that you do more fruitful…”
- Grant Sanderson

Ok, Here’s a quick maths question for you. Raise your hand if you can multiply these two matrices together:

Congratulations if you said:

Now keep your hand up if you know why. And by ‘why’, I don’t mean because:

While mathematically true, this formula is more descriptive of ‘how’ than it is of ‘why’. In and of itself, this formula is pretty much devoid of intuition.
And yet, this is how matrix multiplication is nearly always taught. Memorize the formula. Use it in an exam. Profit? This was certainly my experience, both when first learning linear algebra, and then while attending an ostensibly world-leading university to study for my mathematics bachelors.
What is matrix multiplication really?
Before answering this question, let’s take a step back and think about what a linear transformation is. To keep things simple, let’s keep things in two dimensions (though the following applies to higher dimensions as well).
A linear transformation is a way of changing the shape of a ‘space’ (in this case, the 2D plane), in such a way that:
Keeps parallel lines parallel.
Maintains an equal distance between parallel lines that were equally spaced to begin with.
Leaves the origin at the origin.
Broadly speaking, this gives us three different types of linear transformations that we could do:
Rotations

Scaling (reducing or increasing the space between parallel lines). Note: this also accounts for reflections in either of the x or y axes, these simply have negative scale factors.

Sheers (Note: how this preserves equal distance between parallel lines)

Any combination of these three types of operation would also be a linear transformation on its own terms.
Justifying vector multiplication:
Whilst these illustrations above are created to demonstrate the fact that a linear transformation affects the entirety of 2D space, it transpires that we can describe them in terms of what they do to the two ‘unit vectors’, called î and ĵ respectively.

This is driven by the fact that you can reach any point on the 2D plane with a linear combination of î and ĵ (for example, a vector v [3, -2] will simply be equivalent to 3 lots of î plus -2 lots of ĵ).

Suppose we want to think about a linear transformation that rotates everything counter-clockwise by a quarter turn. What becomes of our vector, v? It turns out we can describe what happens to v purely in terms of what happens to î and ĵ.
Recall that v, [3, -2], was given as 3 lots of î plus -2 lots of ĵ. Well, it turns out that transformed v is equivalent to 3 lots of transformed î plus -2 lots of transformed ĵ.

This line transformed v = 3*[0,1] + (-2)*[-1,0] is “where all the intuition is”.
In particular, we can take the vectors of ‘transformed î’ and ‘transformed ĵ’, put them together to form a 2x2 matrix, refer back to this more ‘intuitive’ view of what happens to v, and all of a sudden we’ve justified vector multiplication.
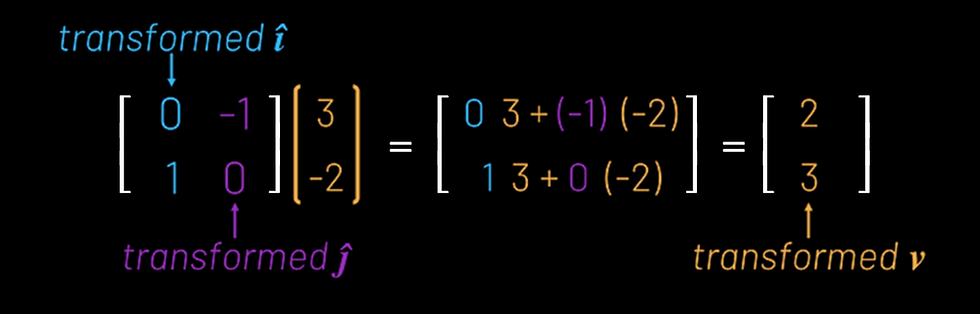
Justifying matrix multiplication:
So what about the multiplication of two 2x2 matrices that we examined earlier?
We’ve just demonstrated that a 2x2 matrix will necessarily represent some kind of linear transformation in 2D space. In particular, for a given matrix [[a, b], [c, d]], the vectors [a, c] and [b, d] represent the coordinates of ‘transformed î’ and ‘transformed ĵ’ respectively.
Suppose we want to make two linear transformations one after the other. For illustration, let’s suppose we perform the counter-clockwise quarter-turn that we looked at before, and follow this with a reflection in the x-axis. These two transformations can be both be represented by 2x2 matrices. We already know the matrix that represents the rotation,
so what about the reflection? We can use the same technique as before — watch what happens to î and ĵ.

So how can we think about the case when two transformations are performed one after another, first the rotation, then the reflection? We can approach this in the same way as before — watch what happens to î and ĵ.
We know from before that the rotation takes î from [1, 0] to [0, 1]. If we then want to apply the reflection to this ‘transformed î’, we simply need to multiply the matrix representing this reflection by the vector representing ‘transformed î’, [0, 1] (recall — we’ve already shown that multiplying a transformation matrix by a vector describes what happens to that vector when transformed).
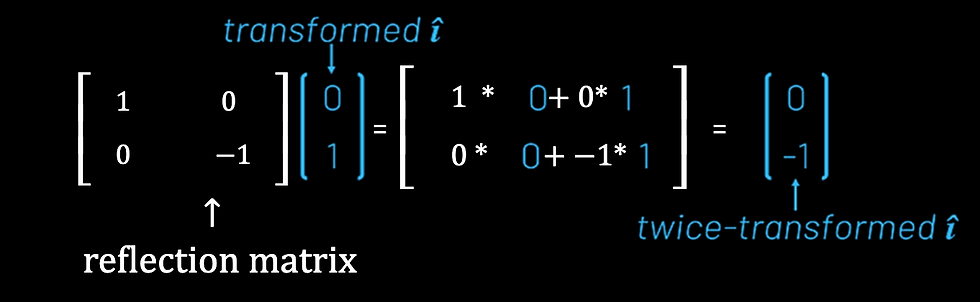
Of course, we now need to observe what happens to ĵ, using the same reasoning.
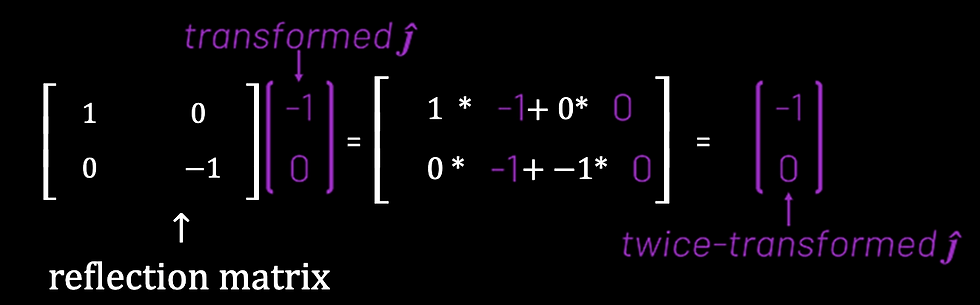
we can put these two vectors together to describe the cumulative effect as a single matrix.

Which looks an awful lot like a representation of our standard formula for matrix multiplication. Of course, you could try this thought experiment with any sequence of linear transformations.
It's a wrap:)
Thanks for reading all the way to the end of the blog!

Commentaires