
Random variables are a cornerstone of probability theory and statistics, providing a bridge between abstract mathematical concepts and real-world phenomena. Their significance spans various fields, including finance, engineering, medicine, and social sciences, where they aid in decision-making, risk assessment, and predictive modeling. This blog delves into the essential role of random variables, emphasizing their importance in statistical analysis and practical applications.
Understanding Random Variables
A random variable is a numerical outcome of a random phenomenon. It assigns a number to each possible outcome of a random process, enabling the quantification and analysis of uncertainty. Random variables can be classified into two main types:
Discrete Random Variables: These take on a countable number of distinct values. Examples include the number of heads in a series of coin tosses or the number of customers arriving at a store in an hour.
Continuous Random Variables: These take on an infinite number of possible values within a given range. Examples include the time taken to run a race or the height of individuals in a population.
Role in Statistical Analysis
Random variables are fundamental to statistical analysis, forming the basis for numerous statistical concepts and methods. Here are some key aspects:
Probability Distributions
A probability distribution describes how the values of a random variable are distributed. For discrete random variables, we use probability mass functions (PMFs), while for continuous random variables, probability density functions (PDFs) are used.
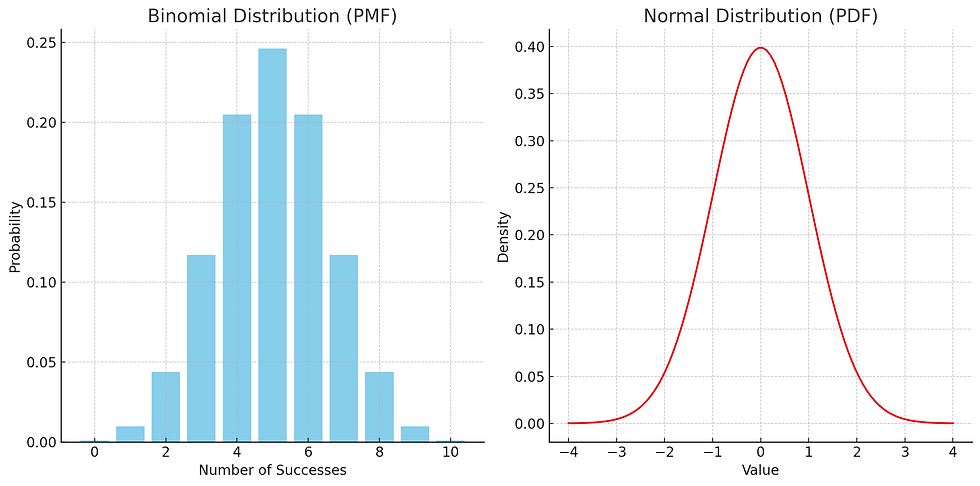
Graph Suggestion: Plot PMF for a binomial distribution and PDF for a normal distribution.
Example: The binomial distribution models the number of successes in a fixed number of independent Bernoulli trials, such as the number of defective items in a batch of products.
Example: The normal distribution, often referred to as the bell curve, models continuous data with a symmetric distribution around the mean, such as human heights or test scores.
Expected Value and Variance
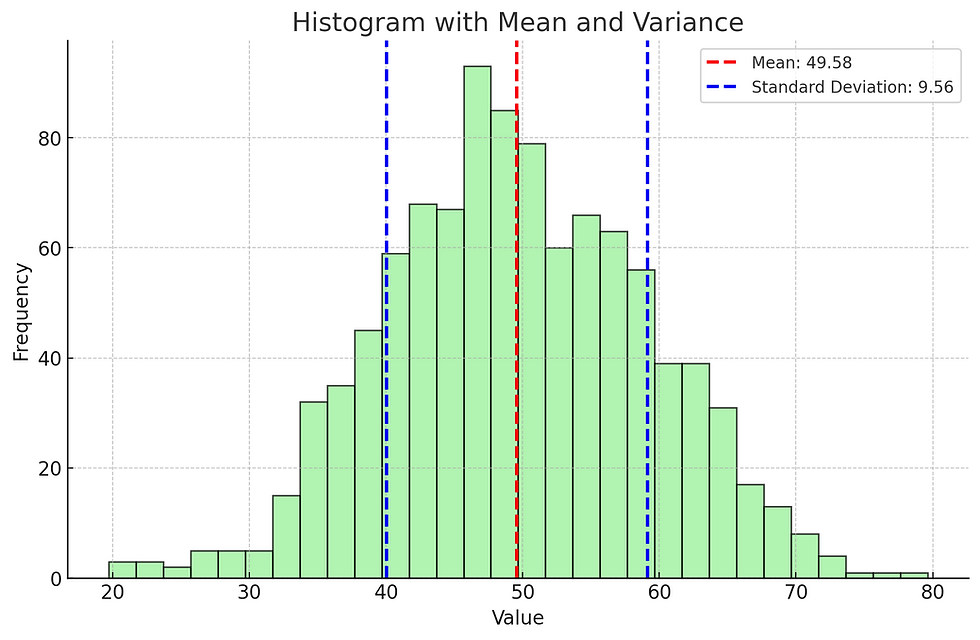
The expected value (mean) of a random variable provides a measure of central tendency, while the variance measures the spread or dispersion of the values around the mean.
Graph Suggestion: Histogram showing sample data with mean and variance indicated.
Example: In finance, the expected return of an investment is a critical metric, while the variance (or standard deviation) is used to assess risk.
Law of Large Numbers
The law of large numbers states that as the sample size increases, the sample mean will converge to the expected value of the population mean. This principle underpins the reliability of statistical estimates.
Graph Suggestion: Line graph showing sample mean converging to the population mean as sample size increases.
Example: In quality control, monitoring large samples of products ensures that the average defect rate aligns closely with the expected defect rate, allowing for better quality assurance.

Real-World Applications
The application of random variables extends across various domains, facilitating data-driven decision-making and predictive modeling.
Finance and Economics
In finance, random variables model the uncertainty and variability of asset prices, interest rates, and economic indicators.
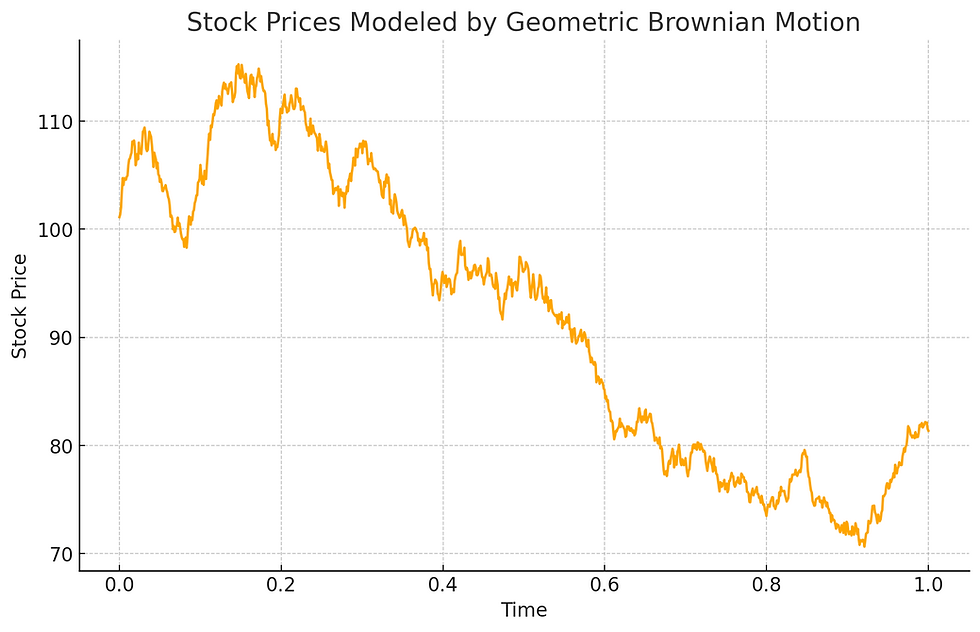
Stock Prices: Stock prices are modeled as random variables, often using geometric Brownian motion. This approach helps in option pricing models like the Black-Scholes model.
Portfolio Theory: The returns on a portfolio of assets are random variables. Modern portfolio theory uses the expected return and variance of these returns to optimize the portfolio's risk-return tradeoff.
Graph Suggestion: Plot showing historical stock price movements modeled by geometric Brownian motion.
Engineering and Quality Control
In engineering, random variables model uncertainties in system performance and material properties, aiding in design and quality assurance.
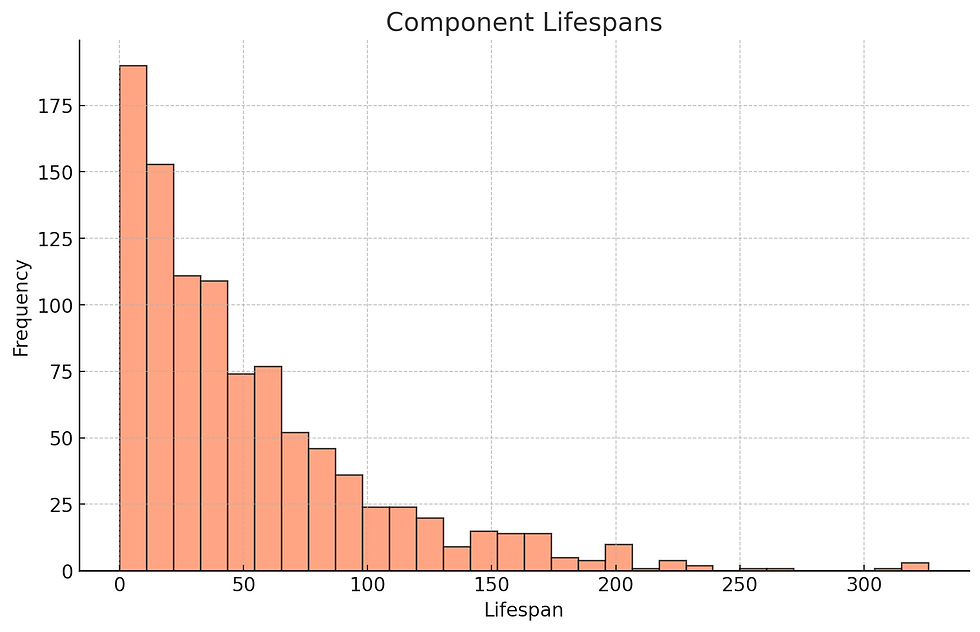
Reliability Engineering: The lifespan of components is modeled using random variables, allowing engineers to predict failure rates and maintenance schedules.
Six Sigma: This quality control methodology relies on statistical measures of process variation, often modeled using normal distributions, to reduce defects and improve product quality.
Graph Suggestion: Probability distribution of component lifespans and Six Sigma control charts.
Medicine and Public Health
In medicine and public health, random variables play a crucial role in understanding the variability in patient responses and disease progression.
Clinical Trials: Patient outcomes in clinical trials are modeled as random variables, enabling the assessment of treatment efficacy and safety.
Epidemiology: The spread of diseases is modeled using random variables, helping public health officials predict outbreaks and allocate resources effectively.
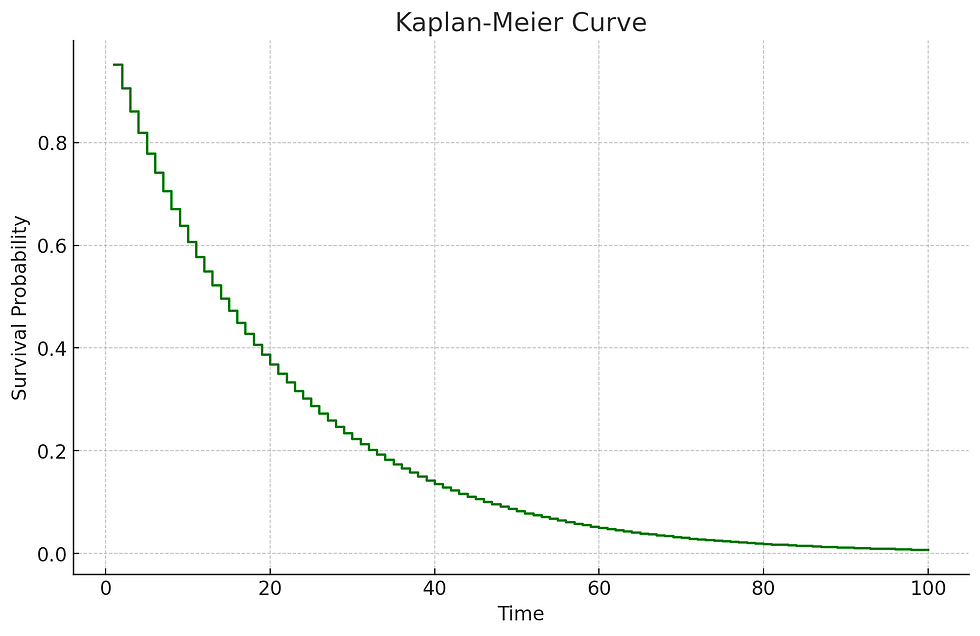
Graph Suggestion: Kaplan-Meier curve for survival analysis in clinical trials.
Social Sciences
In social sciences, random variables help in analyzing human behavior, societal trends, and survey data.
Survey Sampling: Responses in surveys are treated as random variables. Techniques like stratified sampling and regression analysis rely on these variables to draw inferences about the population.
Psychometrics: Scores on psychological tests are modeled as random variables to assess individual differences and validate test reliability.
Conclusion
Random variables are indispensable in bridging the gap between theoretical probability and real-world applications. Their ability to model uncertainty and variability makes them essential in statistical analysis, decision-making, and predictive modeling across diverse fields. As data continues to proliferate in the modern world, the importance of random variables in making sense of this data and deriving actionable insights will only continue to grow. Whether in finance, engineering, medicine, or social sciences, understanding and leveraging random variables is key to navigating the complexities of the real world.
