Unraveling the Web: Probability Behind the Spread of Rumors.
"A rumor without a leg to stand on will get around some other way." - John Tudor

In a world where information travels faster than a click, rumors have found a new realm to thrive—the digital landscape. The probability of a rumor taking root and spreading like wildfire is a fascinating study in human psychology, sociology, and the mechanics of communication. Join us as we delve into the intriguing world of probabilities and unveil the factors that determine the fate of a rumor's journey.
The Seed of Speculation: Every rumor begins with a seed—a fragment of information, a half-truth, or even a complete fabrication. The probability of a rumor spreading is influenced by the nature of this initial seed. The more sensational or emotionally charged it is, the higher the likelihood of it catching on.
The Catalyst of Connectivity: Enter the digital age, where social media platforms act as the catalysts for rumor propagation. The probability of a rumor spreading exponentially increases as it's shared and reshared across networks. Algorithms designed to amplify engaging content play a significant role in boosting the reach of rumors, often beyond our control.
One particularly good tool for explaining the counterintuitive, and seeing if it really is the case, is the mathematical model, and in this instance there is already a group of models to hand. SIR models (Susceptible, Infected, Recovered) are used to study the spread of epidemics and have been adopted and adapted to describe the spread of a rumor; so if someone tells you that a piece of news has spread "like an epidemic" they're closer to the truth than they might think.
Imagine you are in the midst of a class election. To put the electorate off voting for Candidate B, Candidate A has been telling people that their opponent is more invested in his status as teacher's pet than promoting the common good. This is a particularly tactical campaign for a schoolchild, so no-one is cynical about what is being said.
The pupils now fall into three categories: those who know and will pass on the rumor (Spreaders); those who know and won't pass on the rumor (stiflers), and those who don't yet know the rumor (Ignorants). At this point you could argue that a variety of different behaviours will surface in each group, but for simplicity's sake we will limit them to a few basic rules:
At the start there are only Ignorants and Spreaders.
All Ignorants will become Spreaders if and when they first hear the rumor.
All Spreaders will tell the rumor to everyone they meet until they come across either another Spreader, or a Stifler — at this point they will decide that the rumor is known and become a Stifler.
The rumor ends when there are only Ignorants and Stiflers remaining.
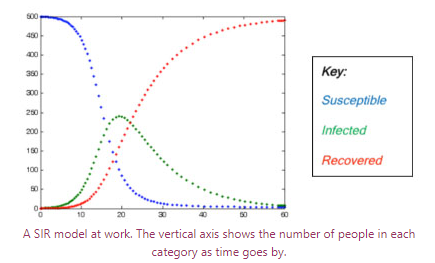
The SIR model gives some idea of how a rumor might spread, but a more pertinent question for anyone who wants to disseminate information quickly is how fast and what's the probability? If we know that, we can make improvements — to the model and real life — to get the news out even faster.
To do so, it is easier to (temporarily) forget about Stiflers and imagine that eventually everyone will know the rumor. An ideal population would be something like that of a small village, where everyone knows each other and gossip spreads like wildfire.
Mathematically this can be modelled by something called a complete graph. A graph is a collection of points (nodes) joined together by a collection of lines (edges). In a complete graph every node is connected to every other node.
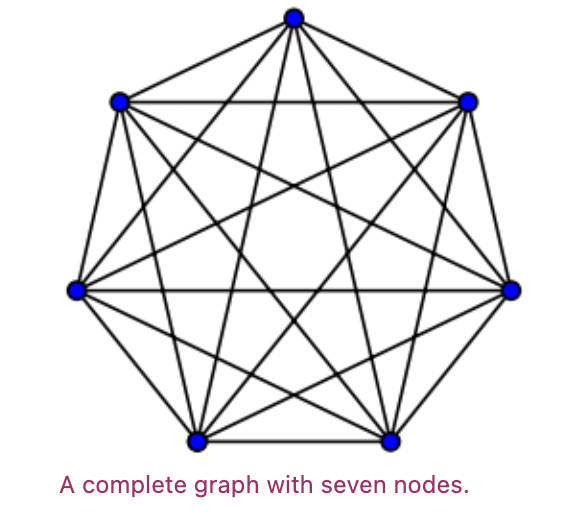
Each point in the graph represents a villager, and the lines depict connections between pairs of villagers. Quite suitably, a collection of points within any network which are all connected (as in a complete graph) is called a clique.
To begin with suppose that only one person is aware of the rumor. Knowing this, you can ask what would happen if any pair of villagers happens to meet in the street, and one has the chance to pass the news on: if they know the rumor, they spread it to the other villager; if not, they don't.
In order to work out how long it takes for a rumor to spread, you need to estimate the probability of any potential exchange between two villagers occurring. As you may have noticed, mathematicians like to keep things (relatively) simple, and in this case that means considering the connections between the villagers, as opposed to considering each individual separately. In other words, it allows you to look at the chance that one particular villager will bump into another and pass on the gossip, as one combined probability which considers both villagers.
For understanding the spread of rumor's probability concept let's see them by considering different scenario and let's learn how do they work?
Let's consider different scenarios where a town consists of (n+1) inhabitants, a person narrates a rumor to a second person, who in turn narrates it to a third person, and so on. At each step the recipient of the rumor is chosen at random from the n available persons, excluding the narrator himself. now we are interested in the probability that the rumor will be told r times without returning to the originator.
In this case as any person can narrate the rumor to any one of the n available persons in n ways, one thing is very clear that,

The originator can tell the rumor to any one of the remaining n persons in n ways and each of the (r - 1) recipient can tell it to any one of the remaining (n - 1) persons (without returning to the originator) in (n-1) ways. Hence,

So,

In the second case we are interested in the probability that the rumor will be told r times without being narrated to any person more than once.
Now, the event that the rumor is told r times without being repeated to any person. In this case the first person (originator) can narrate the rumor to any one of the available n persons; 2nd person can tell it to any one of the remaining (n - 1) persons;..........; the rth person can tell the rumor to any one of the remaining (n - r +1) persons.
Hence the favorable number of cases for the event that the rumor is told r times without being repeated to any person is n (n - 1) (n - 2) .... (n - r + 1).

Now, let's just consider the case when at each step the rumor is told by one person to a gathering of N randomly chosen people without returning to the originator.
In this case when the rumor is told by one person to a gathering of N randomly chosen persons simultaneously,




By following the same argument the probability of the event that the rumor will be told r times without being narrated to any person more than once to a gathering of N people:

Using the probabilities chosen for each interaction — which we take to be all the same — a Mathematical model designed by A.J. Ganesh predicts that on average, for n people, everyone will have heard the news after 2log(n) units of time. What the time units are depends on how quickly the rumor is passed from person to person; it would go faster between rooms on a hotel corridor, for example, than between houses on a street. (The 2log(n) is the expected value, see Ganesh's Paper for details.)
And if you wanted to know how long it would take for everyone in the world to find out about your latest crush, and you only managed to keep the secret for a day, then you should have on average 2 log(7,260,711,000) or 45.4 days to plan your next move (7,260,711,000 was the estimated world population in 2014 according to the World Bank). That is assuming that you are equally close to each of the 7,260,711,000 other people on this planet, and they're all pretty tight too.
The classical model for the spread of a rumor consists of n individuals one of whom, the spreader, knows a rumor. Those individuals who do not know the rumor are called ignorants. On day one the spreader chooses one individual at random, which could be the spreader himself, to whom to tell the rumor. As noted it may not spread the first day. If an ignorant is chosen, the spreader tells the rumor and on the next day there are two spreaders. Each spreader chooses one person at random (which could be himself, the other spreader, or an ignorant) to whom to tell the rumor. This continues until all persons have heard the rumor. if Sn is the minimum time for all ignorants to hear the rumor then
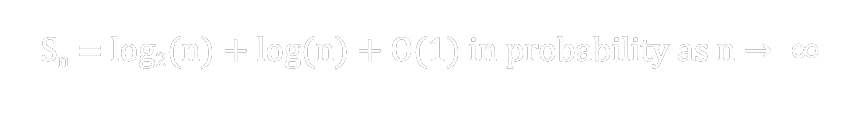
The more general model has three classes of individuals: spreaders (S), ignorants (I), and stiflers (R). Stiflers are individuals who have heard the rumor, but do not spread the rumor. In the case where sampling without replacement is used, a multivariate hypergeometric distribution is used. Two models are considered depending on the interaction of the three groups. In one model all of the ignorants eventually hear the rumor and in the other model a certain percentage of the ignorants fail to hear the rumor, depending on the initial number of spreaders.
Assume the population is size n and suppose on a given day there are k spreaders and hence n−k ignorants. We then take a sample of size k without replacement. Interpreting the n−k ignorants as “successes” then if X is the random variable counting the number of individuals to be told the rumor on the given day. This is the same as counting the number of successes in a sample of size k. Therefore
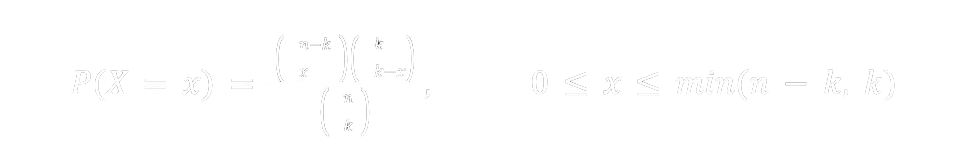
This is the hypergeometric distribution with population size n, n − k successes, and sample size k, which is denoted by HG(n, n − k, k). We have then
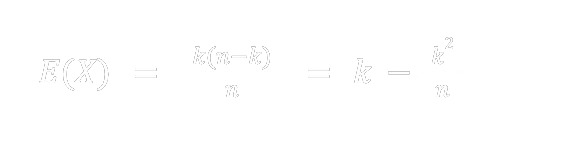
Note that a doubling of the number that have heard the rumor takes place when E(X) > k or k < sqrt(n/2) . For n large, when initially there is one spreader, we expect to have 2^j spreaders after j days when j is small. The following graphs depict simulations of this process of sampling without replacement.
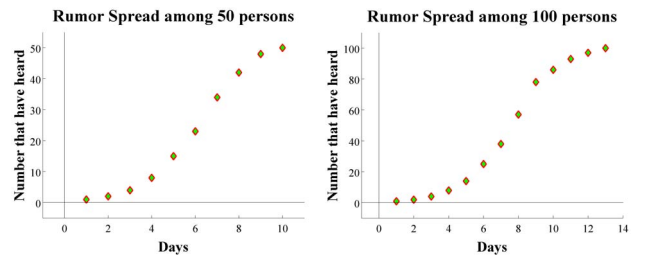
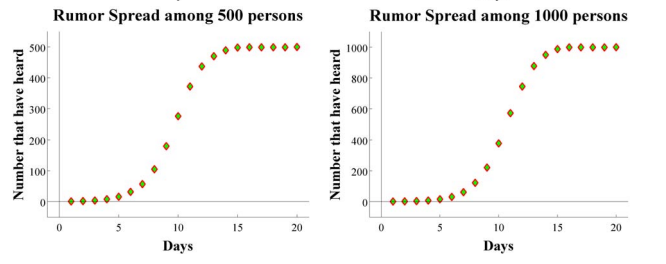
Different simulations produce nearly the same data, but for length of time for all to hear the rumor.
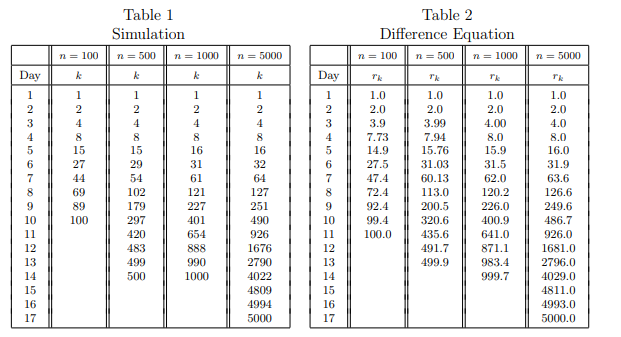
Note that, as expected the number of spreaders doubles early on in the sumulations. We are now interested in finding an expression for how long it takes for the entire population to know the rumor. Let rj be the expected number that know the rumor on day j. Then from the expected value of the hypergeometric distribution we have
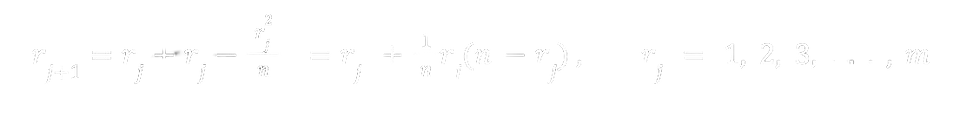
Here m is the number of days for rj to reach n. This is a logistic difference equation and produces similar data (Table 2) as in Table 1. This logistic difference equation is an Euler’s method approximation to the differential equation
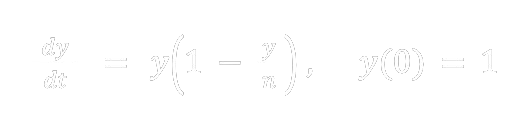
with step size h = 1. Since this is a separable equation the exact solution is found to be
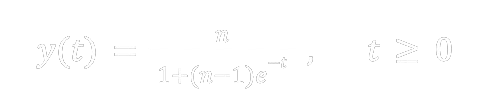
We use this exact solution to estimate m. We want to find the time tn at which y(t) is closest to have the integer value n. So we let 0 < ε < 1/2 and solve the equation y(tn) = n − ε for tn, which yields the solution tn = log ((n − ε)(n − 1)/ε). Here and henceforth, log denotes the natural logarithm. Using the Taylor series for log(1 − x) = −x + x^2/2 + O(x^3 ) where x = ε/n or x = 1/n. Choose n large enough so that |x| < 1,

where c = 2 log 2 ≈ 1.386. For n large the dominant term above is c log(base 2) n and so the time estimate for all of the ignorants to hear the rumor is
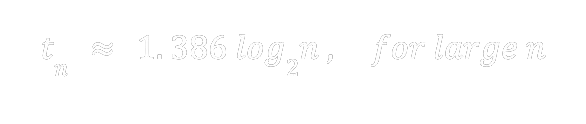
This gives the time estimate in the case of sampling with replacement as approximately 2.443 log n. Thus, a rumor reaches the entire population approximately 1.75 times faster when using sampling without replacement.
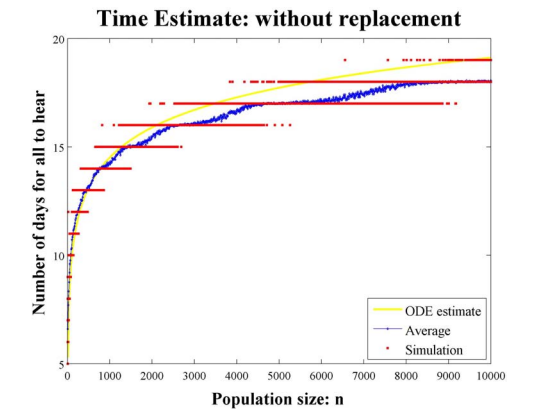
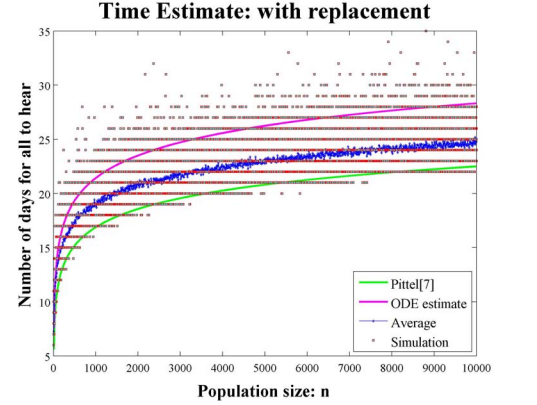
This result shouldn’t be surprising since a spreader is not wasting any time talking to another spreader or two spreaders telling the same ignorant on a given day. When sampling without replacement each spreader is forced to talk to a unique person.
Conclusion:
Using sampling without replacement various models of the spread of a rumor are analyzed. The analysis of these models require the use of both the single variable and multivariate hypergeometric distributions. The spreader-ignorant model produces a system where all the ignorants hear the rumor 1.75 times faster than the classical model.
A common (and often valid) criticism of many mathematical models is that they are too simplified to describe real life well. Though that could be argued for the examples given here, it is not always the case, or indeed, always an issue. While these particular models were chosen for their simplicity, they still give some idea of the way that rumors spread. It is also true that many more complicated models are used every day to inform everything from advertising campaigns to so-called gossip Algorithms which let lots of computers share information quickly.
It's a wrap:)
Thanks for reading all the way to the end of the blog!
