
The Birthday Problem in statistics asks, how many people do you need in a group to have a 50% chance that at least two people will share a birthday?
Go ahead and think about that for a moment. The answer surprises many people. We’ll get to that shortly.
Ok, have you ever noticed how sometimes what seems logical turns out to be proved false with a little math? For instance, how many people do you think it would take to survey, on average, to find two people who share the same birthday? Due to probability, sometimes an event is more likely to occur than we believe it to. In this case, if you survey a random group of just 23 people there is actually about a 50–50 chance that two of them will have the same birthday. This is known as the birthday paradox.
Don't believe it's true? You can test it and see mathematical probability in action!
In this post, we’ll not only answer the birthday paradox, but We’ll also show you how to calculate the probabilities for any size group, and explain why the answer to the Birthday Problem is so surprising.
Calculating Probabilities for the Birthday Problem:
Many people guess 183 because that is half of all possible birthdays, which seems intuitive. Unfortunately, intuition doesn’t work well for solving this problem. So, let’s get straight to calculating probabilities for people sharing birthdays.
For these calculations, we’ll make a few assumptions:
We’ll disregard leap year. That simplifies the math, and it doesn’t change the results by much.
We’ll also assume that all birthdays have an equal probability of occurring.
Let’s start with one person, and then add people in one at a time to illustrate how the calculations work. For these calculations, it is easier to calculate the probability that no one shares a birthday. We’ll then take that probability and subtract it from one to derive the probability that at least two people share a birthday.
Probability of at least one match = 1 – Probability of no match
For the first person, there are no birthdays already covered, which means that there is a 365/365 chance that there is not a shared birthday. That makes sense. We have just one person.
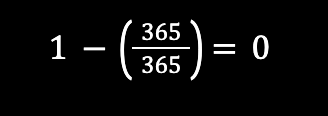
Now, let’s add in the second person, The first person covers one possible birthday, so the second person has a 364/365 chance of not sharing the same day. We need to multiply the probabilities of the first two people and subtract from one.

For the third person, the previous two people cover two dates. Hence, the third person has a probability of 363/365 for not sharing a birthday.

Now, you’re seeing the pattern for how to calculate the probability for a given number of people. Here’s the general form of the equation:

Graphing the Birthday Problem Probabilities
Using Excel, We can calculate and graph the probabilities for any size group.
This graph is made for 70 people:

Conclusion:
By assessing the probabilities, the answer to the Birthday Problem is that you need a group of 23 people to have a 50.73% chance of people sharing a birthday! Most people don’t expect the group to be that small.
Also, notice on the chart that in a room of 75 there’ll be a 99.9% chance of at least two people matching.
It’s virtually guaranteed!
So, HAPPY BIRTHDAY!!
