Which is better – wealth or ability? Fred Mosteller posted this question in his classic 1965 small compendium "Fifty Challenging Problems in Probability", in the context of the Gambler’s Ruin puzzle.

Gambler’s ruin is one of the most essential concepts in Probability theory. The problem involves determining the probability that a gambler wins under the following conditions:
They both start off with a fixed amount of money.
The probability of either one of them winning is constant throughout the game.
The game continues till either one of them runs out of money.
An example would be to considered:
Two gamblers Rahul and Rama. It is given that they start with ₹100 and ₹60 respectively. The gamblers bet on the outcomes of successive coin tosses. If the coin lands head, Rahul wins and Rama has to give ₹1 to Rahul. Else, Rama wins and Rahul has to give ₹1 to Rama. The game continues till one of the players ends up losing all the money. It is also given that the coin is biased, that the probability it lands heads is 1/3. We would now like to determine the probability that Rahul wins the game.
Before we start solving this problem, a couple of things to take note of:
We don’t know how many turns it will take for the game to get over, It is possible that Rama ends up losing every game, and the number of turns would be 60 in such a case. It is also possible that the game never terminates, in the case that each of them wins alternatively. Both of these cases are probable (though very low probability), and so are the infinitely possible other cases between them.
While solving problems in Statistics, it’s often important to identify the problem invariant i.e., something about the problem that’s always going to be constant, something that does not change or depend on outcomes of the sub-problems. For us, the invariant is the total amount of money that the gamblers have. Regardless, of whatever state the game is, the sum of money that Rahul and Rama have is constant: ₹100 + ₹60 = ₹160. The only thing that’s changing is the amount of money that either of the gamblers has. How’s this useful to us? Well, this means that we only need to keep track of the money that one of the gamblers has at any given point in time. The other gambler's money can be obtained by simply subtracting that amount from the total money that both gamblers have (invariant of the game). For instance, if Rahul has ₹85 at some point in the game, we can say that Rama has ₹160- ₹85 = ₹75 at that instance.
These problems are frequently modeled using Markov Chain models. But, in this article, we’ll be using the approach of conditional probability with some modeling techniques to simplify the approach. The key idea is to extend the game into the past and the future to account for different possibilities.
Let’s start by defining some events:
Let R₁₀₀ denote the event that Rahul wins the game given that he starts with ₹100.
Let H denote the event that the coin lands heads on the first flip.
Let T denote the event that the coin lands tails on the first flip
With these definitions, we can define P(R₁₀₀), the probability that Rahul wins the game given that he starts with ₹100 by conditioning it on the outcome of the first flip:
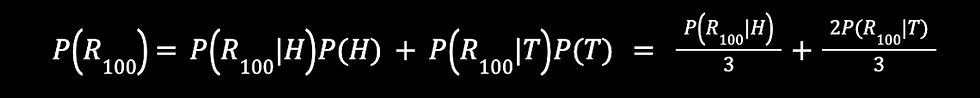
Now, we observe that if Rahul wins in the first game, then Rahul ends up with ₹101. This can be interpreted as exactly the situation that Rahul starts the game with ₹101. Likewise, if Rahul loses in the first game, then he ends up with ₹99. This can be interpreted as exactly the situation that he starts the game with ₹99. Thus, we have:

Thus, we have managed to obtain, something that looks like a recurrence relationship.
What remains is to solve the recurrence relation. To solve this recurrence problem, we need to extend the problem backward and/or forward in time until we reach a base condition i.e., some i such that P(Rᵢ) is known to us. How do we do so?
Well, there are two base conditions that can help us solve the recursive problem:
If it was given to us that Rahul started with ₹0, what can we say about the probability that Rahul wins? Yes, it should be 0! Why? Because if Rahul had no money to start with, he has already lost the game.
If it was given to us that Rahul started with ₹160, what can we say about the probability that Rahul wins? Yes, it should be 1! Why? Because if Rahul had all the money to start with, he has already won the game.
Thus, we have the following pieces of information:

Before solving this recursive problem, we write down the recurrence relationship in a slightly different way to simplify our solution:

Now that we’ve obtained a recurrence relationship and the base condition, we can solve the recurrence formula by tracing the game backward and forward in time.
Sweet! This gives us:

We’ve taken the value of i to go from 1 to 159 because our recurrence relationships will permit a maximum value of i + 1 = 159 + 1 =160 (the maximum amount Rahul can have) and a minimum value of i — 1 = 1–1 = 0 (the minimum amount Rahul can have). We substitute the base case solutions at 0 and 160, to give us the following results:

If we add the first 99 equations (1 ≤ i ≤ 99), we get:

Now, if we know P(R₁), we can calculate P(R₁₀₀) and that will solve our problem!
To find P(R₁), we add all the 159 equations shown previously and use the second base condition that P(R₁₆₀) = 1:

Substituting this result into equation (i), we get:

Some of us might find the result surprising considering that Rahul started with a much higher amount. But, once you realize that the chances of Rahul winning are about half of that of Rama winning at every game, you’ll soon understand why the probability values start to decay exponentially, giving us an almost 0 probability of Rahul winning the game.
In fact, you can generalize the above formula given that Rahul starts with some amount ₹A, and Rama starts with some amount ₹B. If the probability of heads was given to be α, then your recurrence relationship and base cases would be given by:

Solving the above recurrence formula just as before will give us the following solution to the generalized Gamblers Ruin problem:

Note that the above equations holds only as long as α ≠ 0.5. If α = 0.5, the problem becomes quite trivial as the gambler with a higher amount of money is more likely to win since their winning probabilities for each game are the same. In such a situation, the solution would be trivially:

After solving this version of the Gambler’s ruin problem, let’s look at another version of the problem:
Consider two gamblers Rahul and Rama. It is given that they start with ₹100 and ₹60 respectively. The gamblers bet on the outcomes of successive coin tosses. If the coin lands head, Rahul wins and gets ₹1. Else, Rama wins and gets ₹1. The game continues till one of the players gets ₹150. It is also given that the coin is biased, that the probability it lands heads is 1/3. We would now like to determine the probability that Rahul wins the game.
How’s this problem different from the previous problem?
Winning conditions: The winner is now declared as the one who gets ₹150 first.
In-variance: We no longer have the invariance property of the total amount in the game. Since transactions no longer involve a transfer of amount from Rahul to Rama, there could be any indeterminate total amount of money at any point in the game. This means that we’ve to keep track of both the amount that Rahul has and the amount that Rama has at any point in the game.
Note that finding the probability that Rahul wins is the same as determining the probability that Rahul wins 50 games before Rama wins 90 games. So, we model the probabilities as follows:
We let R₍₅₀,₉₀₎ denote the event that Rahul wins 50 games before Rama wins 90 games.
Notice how we track both: the number of gains won by Rahul and those won by Rama (due to the loss of the in-variance property we earlier had). Thus,

Now, we observe that if Rahul wins in the first game, then Rahul needs to win another 49 games. Likewise, if Rama wins in the first game, then Rama needs to win another 89 games. Thus,

Just as before, we may determine the base cases for our recursive problem:
If it was given to us that Rama started with ₹150, (note that this corresponds to R₍₁₅₀,₀₎ what can we say about the probability that Rahul wins? Yes, it should be 0! Why? Because if Rama has ₹150 to start with, Rama has already won the game.
If it was given to us that Rahul started with ₹150, (note that this corresponds to R₍₀,₁₅₀₎ what can we say about the probability that Rahul wins? Yes, it should be 1! Why? Because if Rahul has ₹150 to start with, Rahul has already won the game.
Thus, we have the following pieces of information:

Just as before, we may solve the above recursion problem to obtain the desired probability. However, solving the above problem is much more complex now, given that we’re dealing with two variables to keep track of the number of games each of the players have to win to win the overall gamble.
We get the solution 0.282 to our problem (by software) i.e., the probability that Rahul wins is 0.282, much higher than that in the previous example. This is because every time Rama won meant Rahul lost ₹1 in the previous problem. But, for this problem even if Rama wins one game, Rahul will still be required to win the same number of games to win the overall gamble.
Finally, let’s look at another way to solve this problem, which was earlier suggested by Fermat in his letter to Pascal. This involved modelling the problem as a binomial distribution. Recall that the binomial distribution gives us the probability of k successes in n trials, each success having a probability of p:

How do we model the problem using a binomial distribution? We are asked to find the probability that Rahul wins 50 games before Rama wins 90 games. Thus, if 90 + 50 -1 = 139 games are performed, we are guaranteed to have a winner. Note that this is different from the previous problem as previously there was no limit on the number of tosses. A continuous alteration between Rahul and Rama winning meant a possibility of infinite runs. However, for this problem, since we are guaranteed a winner in 139 games, we can use the binomial distribution to determine the probability of Rahul winning.
Suppose, we extend the game to continue up to 139 tosses. If more than or equal to 50 of these 139 tosses are heads, Rahul wins. Else, Rama wins.
Let X be a random variable for the number of heads in 139 tosses, with each head having a probability of 1/3. Thus:

Thus, the winning probability of Rahul is given by:

Thus, we’ve discussed two versions of the Gamblers Ruin Problem, understood the implications of the problem conditions, and looked at some modeling strategies to solve those problems.
Conclusion (in Mosteller’s words): “It’s better to be twice as good a player than twice as wealthy.”
It's a wrap:)
Thanks for reading all the way to the end of the blog!

Comments